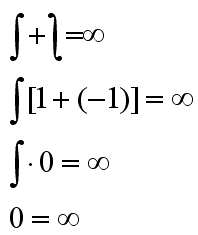Nieskończoność

Nieskończoność, $\infty$ – największa liczba, do której można doliczyć, chociaż nie można do niej doliczyć. Jedyną osobą, ktorej się to udało, jest Chuck Norris.

Jedna z teorii powstania nieskończoności mówi o przesądnych matematykach, którzy napadli i potłukli ósemkę, ponieważ miała być rzekomo mniej szczęśliwa od siódemki. Dlatego też w niektórych kręgach uważa się, że ósemka jest już skończona.

Według niedawno powstałej teorii M&C nieskończoność równa jest 0.

Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam $\int *(1-1)$, co daje 0.

Powstała teoria obala podstawowe zasady współczesnej matematyki.

Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od minus nieskończoności do nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0.

Jednakowoż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera.

Nieskończoność może być większa i mniejsza! To prawo zwie się "Prawem Większej Nieskończoności" lub czasami "Gradacją potencjałów nieskończoności" - Mikołaja Reja, które to prawa spisane i nieudowodnione odnaleziono Pod Lipą! Obecnie mamy szereg przykładów na większe i mniejsze nieskończoności. Jednym z takich przykładów jest ilość prostych przechodzących przez dany punkt! Jeśli taki punkt wyznaczymy na płaszczyźnie "alfa" to przez ten punkt przebiega nieskończenie wiele prostych! Ale jeśli ten sam punkt wyznaczymy w przestrzeni XYZ wówczas również przez taki punkt przebiega nieskończenie wiele prostych ale daleko więcej niż przez punkt położony na płaszczyźnie! Widzimy więc zatem, że nieskończonośc nie równa nieskończoności!!! Podobnych przykładów można znaleźć wiele! Tak więc jeśłi komuś z Państwa przyjdzie do głowy jeszcze inna podobna bzdura, proszę się nie wahać i podzielić się z ludzkością swoimi genialnymi przemyśleniami!

Pozdrawiam