Teoria stożka
Teoria Stożka czyli matematyczny dowód dlaczego tzw. połówka połówką nie jest (kieliszka)
Wstęp i Założenia teoretyczne
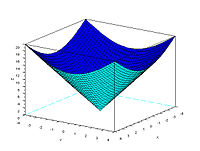
Teoria Stożka zwana również alkoholową teorią stożka jest pierwszym matematycznym dowodem że tzw. połówka (słowo często używane w zwrocie: Nalej mi połówkę) niekoniecznie połówką być musi. Zjawisko picia „połówek” występuje głównie u kobiet, rzadziej u mężczyzn – dzięki Teorii Stożka pełny po brzegi kieliszek też jest połówką. Wynika to z budowy owego naczynia które jest często paraboloidą obrotową – czyli w połowie wysokości tejże przestrzennej figury jest mniej niż połowa objętości jaką można w tej figurze umieścić.
Historia
Twórcą teorii stożka jest Dariusz Wypiór znany jako Pikuś, który przy pomocy młodszego adiunkta wsparcia matematyki stosowanej w oparciu o jego dorobek naukowy Waldemara Kajdasa potwierdził słuszność i celowość tezy. Pierwszy publiczny odczyt miał miejsce w małopolskiej miejscowości Chocznia k/Wadowic w sierpniu 2005 roku. W krótkim czasie od pierwszego odczytu zostało powołanych kilka for dyskusyjnych, na których uczestnicy posługując się aparatem matematycznym jak i empirycznym zgodzili się, a także potwierdziło teorie stożka.
Pomiar szkliwa (Kieliszka)
Do zobrazowania dowodu, który został przedstawiony poniżej został przeprowadzony pomiar cech parametrycznych (wymiarów) kieliszka (quasi-stożka) o równoległych do siebie płaszczyznach dolnej (dna) i górnej. W teorii posługujemy się ściętym stożkiem a nie paraboloidą obrotową, aby ułatwić zrozumienie zagadnienia – Wyniki dla obu tych figur przestrzennych są niemal jednakowe. (Tworząc matematyczny obraz kieliszka jako stożka unikamy wprowadzania bardziej skomplikowanych wzorów).
- Wysokość: H=(5,5±0,1) cm
- Promień podstawy dolnej: r=(0,8±0,1) cm
- Promień podstawy górnej: R=(1,9±0,1) cm
Do dalszych obliczeń błąd miernika (w tym wypadku linijki) nie będzie uwzględniany, gdyż zarówno ten błąd jak i odchyłka od wartości średniej pomiaru jest stosunkowo bardzo mała do spodziewanych wyników i nie wpływa na ostateczny wynik.
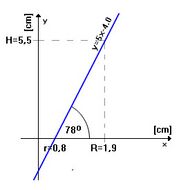
Zmierzone wartości przenosimy na dwuwymiarowy układ współrzędnych (Rys.1). Otrzymując równanie tworzącej stożka y=5x-4. Jako że współczynnik a jest wartością funkcji tangens kąta między osią x a tworzącą otrzymujemy kąt nachylenia tworzącej 78 stopni. Do dowodu przyjmujemy wysokość 9,5 cm gdzie:
- <0cm, 4cm) - Nierzeczywiste przedłużenie stożka tzw. nóżka.
- <4cm, 9,5cm> - Stożek właściwy (mierzalny) tzw. komora wódkowa lub komora szczęścia.
Dowód założeń teoretycznych
W dowodzie właściwym udowodnimy - groteskowo stwierdzając - że "połówka" występuje w każdym miejscu gdzie osoba rozlewająca zachce tę "polówkę" mieć. A ściślej rzecz biorąc formułujemy tezę: „Połowa kieliszka mieści się miedzy jego połową wysokości a całą wysokością”
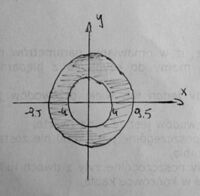
Obliczamy objętość kieliszka (uwzględniając pomiary wyżej zebrane). Objętość V równa się całce potrójnej z jedności po obszarze D. Obszar D dzielimy na dwa: A oraz B. Obszar A składa się z obszarów D2,D4,D5 (Rys. 3) a B z D1,D3. Układ kartezjański zamieniamy na cylindryczny.
Zamiana na zmienne walcowe po obszarze B
Rozwiązanie całki
Zamiana na zmienne walcowe po obszarze A
Rozwiązanie całki
\
Sumaryczna objętość V mierzonego quasi-stożka (kieliszka) wynosi:
Połowa wysokści kieliszka h znajduje się na wysokości 6.75 cm. W sposób analogiczny do przedstawionego powyżej obliczamy objętość połówki dolnej (po obszarach D1;D2) oraz połówki górnej (D3;D4;D5) otrzymując
- Objętość połówki dolnej: Vd = 10.1 ml
- Objętość połówki górnej: Vg = 23.2 ml
- Vd<Vg
Pierwszy wniosek: Połówki nie są sobie równe oraz wniosek drugi - kluczowy - połowa objętości jest zawarta na przedziale względem wysokości od jej połowy do całej wysokości H. Uwzględniając brak przyrządów pomiarowych (mierników) oraz błąd paralaksy ludzkiego oka udowodniliśmy tezę iż nasza "połówka" jest zawarta na przedziale <1/2H,H> w naszym konkretnym badanym przypadku <6.75cm, 9,5cm>
Uwagi
Dysponując aparatem matematycznym a konkretnie rachunkiem całkowym udowodniliśmy słuszność i prawdziwość tezy. Przedstawiona teoria dla samej matematyki i nauk pokrewnych nie jest ważna i istotna, lecz ma duże znaczenie społeczne. Bardzo dobrze sprawdza się tam gdzie w określonej przestrzeni i w określonym czasie znajduje się wiele osób w celu zamierzonej konsumpcji. Należy brać pod uwagę, że teoria jest prawdziwa dla kieliszków w kształcie paraboloidy obrotowej lub stożka (Kieliszki o tworzącej nachylonej pod kątem 0-30 stopni względem osi symetrii najlepiej nadają się do sporzywania płynów). Dla kieliszków typowo cylindrycznych traci sens.






![{\displaystyle \int \limits _{0}^{2\pi }d\varphi \int \limits _{0.8}^{1.9}[\varphi h]_{5\rho }^{9.5}d\rho =\int \limits _{0}^{2\pi }d\varphi \int \limits _{0.8}^{1.9}({9.5\rho }-{5\rho ^{2}})d\rho =}](https://nonsa.pl/api/rest_v1/media/math/render/svg/a95cc387b596f1850ee4d5c4ef172753f7c3c753)
![{\displaystyle =2\pi [({{9.5*1.9^{2}} \over 2}-{{5*1.9^{3}} \over 3})-({{9.5*0.8^{2}} \over 2}-{{5*0.8^{3}} \over 3})]=22.2}](https://nonsa.pl/api/rest_v1/media/math/render/svg/95edfdd8771026ac1566a597e4761889e4f481a5)



![{\displaystyle \int \limits _{0}^{2\pi }d\varphi \int \limits _{0}^{0.8}[\varphi h]_{4}^{9.5}d\rho =\int \limits _{0}^{2\pi }d\varphi \int \limits _{0}^{0.8}({9.5\rho }-{4\rho })d\rho =2\pi [{{5.5\rho ^{2}} \over 2}]_{0}^{0.8}=11.1}](https://nonsa.pl/api/rest_v1/media/math/render/svg/744bdee7b773024b442fdce0b0045f3b55e840f8)

