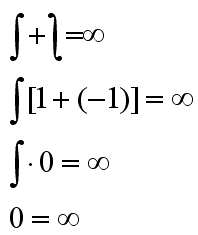Nieskończoność: Różnice pomiędzy wersjami
M (pusty to by był od +0 do -0) |
M (robot dodaje: de, en, fi, he, it, ja, pt) |
||
| Linia 18: | Linia 18: | ||
[[Kategoria:Teorie]] |
[[Kategoria:Teorie]] |
||
[[Kategoria:Matematyka]] |
[[Kategoria:Matematyka]] |
||
[[de:Unendlich]] |
|||
[[en:Infinity]] |
|||
[[fi:Ääretön]] |
|||
[[he:אינסוף]] |
|||
[[it:Infinito]] |
|||
[[ja:無限]] |
|||
[[pt:Infinito]] |
|||
Wersja z 09:46, 19 sie 2007
Jedna z teorii powstania nieskończoności mówi o przesądnych matematykach, którzy napadli i potłukli ósemkę ponieważ, jakoby miała być mniej szczęśliwa od siódemki. Toteż w niektórych kręgach uważa się, że ósemka jest już skończona.
Według niedawno powstałej teorii M&C nieskończoność równa jest 0.
Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam całka * (1-1), co daje 0.
Powstała teoria obala podstawowe zasady współczesnej matematyki.
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od -nieskończoności do +nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0.
Jednakowóż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera.