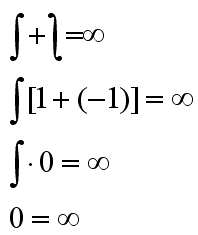Nieskończoność: Różnice pomiędzy wersjami
M (Przywrócono przedostatnią wersję, jej autor to Laurusnobilis. Autor wycofanej wersji to 89.230.27.57.) |
|||
| Linia 7: | Linia 7: | ||
[[Grafika:Matma.PNG]] |
[[Grafika:Matma.PNG]] |
||
Ale potem dodajemy do nieskończoności swoje fiuty i wychodzi fiutokonczonowsc |
|||
Powstała teoria obala podstawowe zasady współczesnej matematyki. |
Powstała teoria obala podstawowe zasady współczesnej matematyki. |
||
Zbiór R jest bowiem zbiorem obustronnie |
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od -nieskończoności do +nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0. |
||
sssssssssss |
|||
Jednakowóż gdyby przedstawić oś |
Jednakowóż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera. |
||
sddddddddddd |
|||
{{stubmat}} |
{{stubmat}} |
||
[[ |
[[Kategoria:Teorie]] |
||
[[Kategoria:Matematyka]] |
[[Kategoria:Matematyka]] |
||
Wersja z 23:07, 30 lis 2007
Jedna z teorii powstania nieskończoności mówi o przesądnych matematykach, którzy napadli i potłukli ósemkę ponieważ, jakoby miała być mniej szczęśliwa od siódemki. Toteż w niektórych kręgach uważa się, że ósemka jest już skończona.
Według niedawno powstałej teorii M&C nieskończoność równa jest 0.
Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam całka * (1-1), co daje 0.
Powstała teoria obala podstawowe zasady współczesnej matematyki.
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od -nieskończoności do +nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0.
Jednakowóż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera.