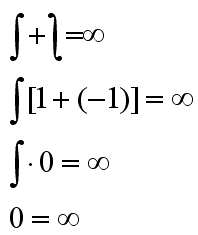Nieskończoność: Różnice pomiędzy wersjami
M (Przywrócono przedostatnią wersję, jej autor to Kracok. Autor wycofanej wersji to 93.157.119.210.) |
Grzeeesiek (dyskusja • edycje) M (Wycofano ostatnie edycje użytkownika 178.43.182.175, powód: oklepane) Znacznik: rewert |
||
| (Nie pokazano 41 wersji utworzonych przez 35 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''Nieskończoność''', '''<math>\infty</math>''' – największa liczba, do której można doliczyć, chociaż nie można do niej doliczyć. Jedyną osobą, ktorej się to udało, jest Chuck Norris. |
'''Nieskończoność''', '''<math>\infty</math>''' – największa liczba, do której można doliczyć, chociaż nie można do niej doliczyć. Jedyną osobą, ktorej się to udało<ref>I to trzykrotnie!</ref>, jest [[Chuck Norris]], który liczył od minus nieskończoności. |
||
Jedna z teorii powstania nieskończoności mówi o [[przesąd]]nych [[matematyk]]ach, którzy napadli i potłukli ósemkę, ponieważ miała być rzekomo mniej szczęśliwa od siódemki. Dlatego też w niektórych kręgach uważa się, że ósemka jest już skończona. |
Jedna z teorii powstania nieskończoności mówi o [[przesąd]]nych [[matematyk]]ach, którzy napadli i potłukli ósemkę, ponieważ miała być rzekomo mniej szczęśliwa od siódemki. Dlatego też w niektórych kręgach uważa się, że ósemka jest już skończona. |
||
| Linia 7: | Linia 7: | ||
Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam <math>\int* (1-1)</math>, co daje 0. |
Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam <math>\int* (1-1)</math>, co daje 0. |
||
[[ |
[[Plik:Matma.PNG]] |
||
Powstała teoria obala podstawowe zasady współczesnej matematyki. |
Powstała teoria obala podstawowe zasady współczesnej matematyki<ref>W związku z powyższym także wszystkie inne</ref><ref>To właśnie dzięki tej teorii, wiedząc że najlepszym przykładem nieskończoności jest ludzka głupota, potwierdzono, że wszyscy ludzie są inteligentni, bo głupota jest równa 0</ref>. |
||
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od minus nieskończoności do nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0. |
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od minus nieskończoności do nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0. |
||
Jednakowoż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera. |
Jednakowoż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera. |
||
Ostatnio kozaki z kanału Numberphile podali, że suma nieskończoności jest równa -1/12<ref>http://www.youtube.com/watch?v=w-I6XTVZXww</ref>. |
|||
== Zobacz też == |
== Zobacz też == |
||
| Linia 20: | Linia 22: | ||
* [[Nieskończony tunel]] |
* [[Nieskończony tunel]] |
||
{{ |
{{przypisy}} |
||
{{stub|mat}} |
|||
{{Matematyka}} |
|||
[[Kategoria:Teorie]] |
[[Kategoria:Teorie]] |
||
Aktualna wersja na dzień 16:02, 25 paź 2022
Nieskończoność, – największa liczba, do której można doliczyć, chociaż nie można do niej doliczyć. Jedyną osobą, ktorej się to udało[1], jest Chuck Norris, który liczył od minus nieskończoności.
Jedna z teorii powstania nieskończoności mówi o przesądnych matematykach, którzy napadli i potłukli ósemkę, ponieważ miała być rzekomo mniej szczęśliwa od siódemki. Dlatego też w niektórych kręgach uważa się, że ósemka jest już skończona.
Według niedawno powstałej teorii M&C nieskończoność równa jest 0.
Udowodnić to można bardzo prosto za pomocą całkowania. Jak wiemy całka i odwrotność całki (całka obrócona o 180 stopni) złączone ze sobą dają uniwersalny symbol nieskończoności. Po wyciągnięciu całki przed nawias wychodzi nam , co daje 0.
Powstała teoria obala podstawowe zasady współczesnej matematyki[2][3].
Zbiór R jest bowiem zbiorem obustronnie niedomkniętym od minus nieskończoności do nieskończoności. Przy założeniu że nieskończoność to 0, zbiór R jest zbiorem od -0 do +0, czyli zbiorem jednoelementowym zawierającym liczbę 0.
Jednakowoż gdyby przedstawić oś zbioru R za pomocą okręgu można przyjąć że jest to zbiór punktów równoodległych od zera, a zatem każda liczba jest jednocześnie większa i mniejsza od zera.
Ostatnio kozaki z kanału Numberphile podali, że suma nieskończoności jest równa -1/12[4].
Zobacz też[edytuj • edytuj kod]
Przypisy
- ↑ I to trzykrotnie!
- ↑ W związku z powyższym także wszystkie inne
- ↑ To właśnie dzięki tej teorii, wiedząc że najlepszym przykładem nieskończoności jest ludzka głupota, potwierdzono, że wszyscy ludzie są inteligentni, bo głupota jest równa 0
- ↑ http://www.youtube.com/watch?v=w-I6XTVZXww
To jest tylko zalążek artykułu z dziedziny matematyki. Jeśli rozwiązywanie różniczek to twoje ulubione zajęcie – rozbuduj go.
