Geometria wykreślna: Różnice pomiędzy wersjami
(nowa strona) |
Ostrzyciel (dyskusja • edycje) M |
||
| (Nie pokazano 16 wersji utworzonych przez 13 użytkowników) | |||
| Linia 1: | Linia 1: | ||
[[Plik:Sklepienie-Model.png|200px|thumb |
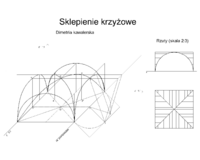
[[Plik:Sklepienie-Model.png|200px|thumb|Przykładowe zadanie z geometrii wykreślnej – dimetria kawalerska<ref>Rodzaj aksonometrii</ref> i rzuty Monge'a sklepienia krzyżowego otwartego<ref>Autor był leniwy i użył [[komputer|narzędzia Szatana]] zamiast rysować ręcznie</ref>]] |
||
{{cytat| |
{{cytat|My wiemy, że wam się to do niczego nie przyda, ale pomoże wam rozwinąć wyobraźnię.|Przeciętny wykładowca '''geometrii wykreślnej''' o swoim przedmiocie}} |
||
{{cytat|Wyszedł jakiś [[dziadek]], coś tam pogadał i poszedł, ale nikt nie wie o co mu chodziło.|Przeciętny student o wykładzie z '''geometrii wykreślnej'''}} |
|||
'''Geometria wykreślna''' – dział [[geometria|geometrii]] wykładany na niektórych kierunkach na wyższych uczelniach technicznych w Polsce, krajach byłego [[ZSRR]] i trzeciego świata. Jedyny dział geometrii, do którego nauki wystarczy posiadać jedynie podstawową znajomość algebry. Brzmi fajnie? Każdemu tak |
'''Geometria wykreślna''' – dział [[geometria|geometrii]] wykładany na niektórych kierunkach na wyższych uczelniach technicznych w Polsce, krajach byłego [[Związek Socjalistycznych Republik Radzieckich|ZSRR]] i [[Zimbabwe|trzeciego świata]]. Jedyny dział geometrii, do którego nauki wystarczy posiadać jedynie podstawową znajomość algebry. Brzmi fajnie? Każdemu tak się na początku wydaje. |
||
== Co to w ogóle jest i po co? == |
== Co to w ogóle jest i po co? == |
||
Geometrię wykreślną wynalazł w XVIII w. pewien znudzony matematyk, Gaspard Monge, który bardzo chciał, żeby jakaś dziedzina wiedzy została nazwana jego imieniem |
Geometrię wykreślną wynalazł w XVIII w. pewien znudzony matematyk, Gaspard Monge, który bardzo chciał, żeby jakaś dziedzina wiedzy została nazwana jego imieniem<ref>Inne przejawy tej megalomanii to choćby mechanika Lagrange'a czy algebra Boole'a</ref>. No dobra, w zasadzie ludzie kreślili różne rzeczy już wcześniej, ale dopiero Monge nadał tej dziedzinie wymiar nauki. Generalnie cała rzecz polega na kreśleniu skomplikowanych, najczęściej niezrozumiałych dla nikogo poza rysującym bazgrołów przy użyciu ołówka<ref>Tak, nawet pozwalają korzystać z narzędzia do pisania!</ref>, cyrkla i linijki bez podziałki. Czy o czymś zapomniałem? A tak. Jeszcze kartka jest. |
||
Natomiast pojawia się pytanie po co właściwie bawić się w rysowanie czegokolwiek ręcznie skoro są programy dzięki którym można to zrobić znacznie szybciej? Pytani o to wykładowcy przedmiotu najczęściej w panice załamują ręce i możliwie szybko rysują na najbliższej kartce pieczęć jakiegoś wyjątkowo nieprzyjemnego [[demon]]a w celu napuszczenia go na napastliwego [[student]]a. Czasem zdarza się |
Natomiast pojawia się pytanie: po co właściwie bawić się w rysowanie czegokolwiek ręcznie, skoro są programy dzięki którym można to zrobić znacznie szybciej? Pytani o to wykładowcy przedmiotu najczęściej w panice załamują ręce i możliwie szybko rysują na najbliższej kartce pieczęć jakiegoś wyjątkowo nieprzyjemnego [[demon]]a w celu napuszczenia go na napastliwego [[student]]a. Czasem zdarza się usłyszeć również enigmatyczną odpowiedź o ćwiczeniu wyobraźni, ale tak mówi tylko zdecydowana mniejszość. |
||
== Działy geometrii wykreślnej == |
== Działy geometrii wykreślnej == |
||
[[Plik:Astaroth.svg |
[[Plik:Astaroth.svg|200 px|thumb|Przykład zalecany jako ćwiczenie do działu ''Podstawowe konstrukcje geometryczne'']] |
||
* '''Podstawowe konstrukcje geometryczne''' – czyli zasadniczo to, co student powinien umieć po ukończeniu [[liceum]]. Wliczamy w to proste prostopadłe i równoległe, podział odcinka na części, rysowanie wielokątów foremnych oraz konstrukcję paraboli czy innej elipsy<ref>Jak to nie wiesz jak konstruować elipsę? To w podstawówce było...</ref>. Ogólnie rzecz biorąc nuda, ale i tak nikt najczęściej nie umie tego zrobić od ręki. |
* '''Podstawowe konstrukcje geometryczne''' – czyli zasadniczo to, co student powinien umieć po ukończeniu [[liceum ogólnokształcące|liceum]]. Wliczamy w to proste prostopadłe i równoległe, podział odcinka na części, rysowanie wielokątów foremnych oraz konstrukcję paraboli czy innej elipsy<ref>Jak to nie wiesz jak konstruować elipsę? To w podstawówce było...</ref>. Ogólnie rzecz biorąc nuda, ale i tak nikt najczęściej nie umie tego zrobić od ręki. |
||
* '''Rzut środkowy''' – mówiąc w skrócie perspektywa. Zaczyna się to od rysowania niewinnie wyglądających kółeczek i prostych. Zabawnie zaczyna się jednak kiedy przychodzi do reprezentacji płaszczyzny w rzucie. Ta bowiem przedstawiana jest przez dwie proste, tzw. ślad zbiegu i ślad tłowy. W oparciu o okrąg tłowy i ślady płaszczyzny możemy wyznaczyć np. perspektywę figury przestrzennej. W tym celu musimy wyznaczyć dwa dodatkowe ślady zbiegu na przecięciu śladu zbiegu płaszczyzny i okręgu tłowego. Aby jednak dzieło było kompletne wypada umieć mu zadać jeszcze konkretne wymiary. Wysokość odmierzamy normalnie jako odcinek pionowy od śladu tłowego, a odcinek podstawy jako położony na śladzie tłowym i następnie rzutujemy do właściwego śladu zbiegu. Wydaje się proste? To teraz weź to narysuj i wspomóż artykuł grafiką. |
* '''Rzut środkowy''' – mówiąc w skrócie perspektywa. Zaczyna się to od rysowania niewinnie wyglądających kółeczek i prostych. Zabawnie zaczyna się jednak kiedy przychodzi do reprezentacji płaszczyzny w rzucie. Ta bowiem przedstawiana jest przez dwie proste, tzw. ślad zbiegu i ślad tłowy. W oparciu o okrąg tłowy i ślady płaszczyzny możemy wyznaczyć np. perspektywę figury przestrzennej. W tym celu musimy wyznaczyć dwa dodatkowe ślady zbiegu na przecięciu śladu zbiegu płaszczyzny i okręgu tłowego. Aby jednak dzieło było kompletne, wypada umieć mu zadać jeszcze konkretne wymiary. Wysokość odmierzamy normalnie jako odcinek pionowy od śladu tłowego, a odcinek podstawy jako położony na śladzie tłowym i następnie rzutujemy do właściwego śladu zbiegu. Wydaje się proste? To teraz weź to narysuj i wspomóż artykuł grafiką. |
||
* '''Aksonometria''' – najprostszy dział tego czegoś. Zasadniczo wystarczy umieć wrysować figurę w trójwymiarowy układ współrzędnych. Żeby jednak nie było za prosto wersji układów współrzędnych jest kilka i różnią się skrótem długości na poszczególnych osiach i kątem ich rozwarcia. |
* '''Aksonometria''' – najprostszy dział tego czegoś. Zasadniczo wystarczy umieć wrysować figurę w trójwymiarowy układ współrzędnych. Żeby jednak nie było za prosto, wersji układów współrzędnych jest kilka i różnią się skrótem długości na poszczególnych osiach i kątem ich rozwarcia. |
||
* '''Rzuty Monge'a''' – co prawda panu Monge'owi nie udało się dorobić własnej dziedziny geometrii, ale tutaj się uchował. Cała zabawa polega na narysowaniu dwóch lub trzech rzutów zadanej figury (od góry, od przodu i ewentualnie prawy bok). Może to i proste, ale tylko do momentu, gdy nie musimy zastanawiać się nad widocznością przekroju półwalca przeciętego konoidą paraboliczną. |
* '''Rzuty Monge'a''' – co prawda panu Monge'owi nie udało się dorobić własnej dziedziny geometrii, ale tutaj się uchował. Cała zabawa polega na narysowaniu dwóch lub trzech rzutów zadanej figury (od góry, od przodu i ewentualnie prawy bok). Może to i proste, ale tylko do momentu, gdy nie musimy zastanawiać się nad widocznością przekroju półwalca przeciętego konoidą paraboliczną. |
||
* '''Rzut cechowany''' – prostszy od rzutu Monge'a, bo wykonuje się tylko jeden rysunek (od góry) i nanosi współrzędną wysokości punktu. Standardowym przykładem takiego rzutu jest mapa wysokościowa (hipsometryczna). Paradoks polega jednak na tym, że student najpierw ma za zadanie narysować mapę na [[geodezja|geodezji]], a dopiero potem dowiaduje się, że nazywa się to rzut cechowany i jest wykreślane według jakichś tam zasad. |
* '''Rzut cechowany''' – prostszy od rzutu Monge'a, bo wykonuje się tylko jeden rysunek (od góry) i nanosi współrzędną wysokości punktu. Standardowym przykładem takiego rzutu jest mapa wysokościowa (hipsometryczna). Paradoks polega jednak na tym, że student najpierw ma za zadanie narysować mapę na [[geodezja|geodezji]], a dopiero potem dowiaduje się, że nazywa się to rzut cechowany i jest wykreślane według jakichś tam zasad. |
||
== Jak to wygląda w praktyce? == |
== Jak to wygląda w praktyce? == |
||
[[Plik:Scan.png|200 px|thumb|Znajdź błąd<ref>Tak, tu naprawdę jest błąd</ref>]] |
|||
W praktyce nie wygląda to wcale, bo nikt nie jest w stanie zrozumieć o czym właściwie mówi dziadek czy ewentualnie [[babcia]]<ref>Ten przedmiot wykładają tylko niespełnieni architekci po sześćdziesiątce |
W praktyce nie wygląda to wcale, bo nikt nie jest w stanie zrozumieć o czym właściwie mówi dziadek czy ewentualnie [[babcia]]<ref>Ten przedmiot wykładają tylko niespełnieni architekci po sześćdziesiątce lub matematycy, którym całki pożarły mózg</ref> prowadząca przedmiot. Dlatego też pierwsze kolokwium wzbudza niesłychane emocje, a studenci porzucają [[piwo]] i [[Dziewczyna|dziewczyny]], żeby zasiąść do książek nazywanych np. ''Geometria wykreślna. Podręcznik dla opornych''. Napełnieni poczuciem wiedzy ruszają następnie na [[Uczelnia|uczelni]]ę celem napisania kolokwium. To zaś najczęściej utwierdza ich w przekonaniu, że wszystko jest łatwe. Bomba wybucha dopiero, gdy dochodzi do podania wyników prac. I w ogóle ''to czego pan jeszcze ode mnie chce? Tu jest taka plamka, o. A jej nie powinno być. To zaburza odbiór rysunku. I te rzuty jeszcze takie nieciekawe. Czternaście punktów<ref>Na możliwe na przykład 33.</ref> to i tak za dużo jak na taką brzydką pracę.'' |
||
== Zobacz też == |
|||
* [[teoria stożka]] (twierdzenie o połówce kieliszka) |
|||
* [[kwadratura koła]] |
|||
* [[sześcian]] |
|||
* …a jak nie masz wykreślnej na studiach, to może przynajmniej jest [[mechanika płynów]]? |
|||
{{Przypisy}} |
{{Przypisy}} |
||
{{Budownictwo}} |
|||
{{Matematyka}} |
|||
[[Kategoria:Geometria]] |
[[Kategoria:Geometria]] |
||
Aktualna wersja na dzień 17:46, 26 paź 2020
My wiemy, że wam się to do niczego nie przyda, ale pomoże wam rozwinąć wyobraźnię.
- Przeciętny wykładowca geometrii wykreślnej o swoim przedmiocie
Wyszedł jakiś dziadek, coś tam pogadał i poszedł, ale nikt nie wie o co mu chodziło.
- Przeciętny student o wykładzie z geometrii wykreślnej
Geometria wykreślna – dział geometrii wykładany na niektórych kierunkach na wyższych uczelniach technicznych w Polsce, krajach byłego ZSRR i trzeciego świata. Jedyny dział geometrii, do którego nauki wystarczy posiadać jedynie podstawową znajomość algebry. Brzmi fajnie? Każdemu tak się na początku wydaje.
Co to w ogóle jest i po co?[edytuj • edytuj kod]
Geometrię wykreślną wynalazł w XVIII w. pewien znudzony matematyk, Gaspard Monge, który bardzo chciał, żeby jakaś dziedzina wiedzy została nazwana jego imieniem[3]. No dobra, w zasadzie ludzie kreślili różne rzeczy już wcześniej, ale dopiero Monge nadał tej dziedzinie wymiar nauki. Generalnie cała rzecz polega na kreśleniu skomplikowanych, najczęściej niezrozumiałych dla nikogo poza rysującym bazgrołów przy użyciu ołówka[4], cyrkla i linijki bez podziałki. Czy o czymś zapomniałem? A tak. Jeszcze kartka jest.
Natomiast pojawia się pytanie: po co właściwie bawić się w rysowanie czegokolwiek ręcznie, skoro są programy dzięki którym można to zrobić znacznie szybciej? Pytani o to wykładowcy przedmiotu najczęściej w panice załamują ręce i możliwie szybko rysują na najbliższej kartce pieczęć jakiegoś wyjątkowo nieprzyjemnego demona w celu napuszczenia go na napastliwego studenta. Czasem zdarza się usłyszeć również enigmatyczną odpowiedź o ćwiczeniu wyobraźni, ale tak mówi tylko zdecydowana mniejszość.
Działy geometrii wykreślnej[edytuj • edytuj kod]
- Podstawowe konstrukcje geometryczne – czyli zasadniczo to, co student powinien umieć po ukończeniu liceum. Wliczamy w to proste prostopadłe i równoległe, podział odcinka na części, rysowanie wielokątów foremnych oraz konstrukcję paraboli czy innej elipsy[5]. Ogólnie rzecz biorąc nuda, ale i tak nikt najczęściej nie umie tego zrobić od ręki.
- Rzut środkowy – mówiąc w skrócie perspektywa. Zaczyna się to od rysowania niewinnie wyglądających kółeczek i prostych. Zabawnie zaczyna się jednak kiedy przychodzi do reprezentacji płaszczyzny w rzucie. Ta bowiem przedstawiana jest przez dwie proste, tzw. ślad zbiegu i ślad tłowy. W oparciu o okrąg tłowy i ślady płaszczyzny możemy wyznaczyć np. perspektywę figury przestrzennej. W tym celu musimy wyznaczyć dwa dodatkowe ślady zbiegu na przecięciu śladu zbiegu płaszczyzny i okręgu tłowego. Aby jednak dzieło było kompletne, wypada umieć mu zadać jeszcze konkretne wymiary. Wysokość odmierzamy normalnie jako odcinek pionowy od śladu tłowego, a odcinek podstawy jako położony na śladzie tłowym i następnie rzutujemy do właściwego śladu zbiegu. Wydaje się proste? To teraz weź to narysuj i wspomóż artykuł grafiką.
- Aksonometria – najprostszy dział tego czegoś. Zasadniczo wystarczy umieć wrysować figurę w trójwymiarowy układ współrzędnych. Żeby jednak nie było za prosto, wersji układów współrzędnych jest kilka i różnią się skrótem długości na poszczególnych osiach i kątem ich rozwarcia.
- Rzuty Monge'a – co prawda panu Monge'owi nie udało się dorobić własnej dziedziny geometrii, ale tutaj się uchował. Cała zabawa polega na narysowaniu dwóch lub trzech rzutów zadanej figury (od góry, od przodu i ewentualnie prawy bok). Może to i proste, ale tylko do momentu, gdy nie musimy zastanawiać się nad widocznością przekroju półwalca przeciętego konoidą paraboliczną.
- Rzut cechowany – prostszy od rzutu Monge'a, bo wykonuje się tylko jeden rysunek (od góry) i nanosi współrzędną wysokości punktu. Standardowym przykładem takiego rzutu jest mapa wysokościowa (hipsometryczna). Paradoks polega jednak na tym, że student najpierw ma za zadanie narysować mapę na geodezji, a dopiero potem dowiaduje się, że nazywa się to rzut cechowany i jest wykreślane według jakichś tam zasad.
Jak to wygląda w praktyce?[edytuj • edytuj kod]
W praktyce nie wygląda to wcale, bo nikt nie jest w stanie zrozumieć o czym właściwie mówi dziadek czy ewentualnie babcia[7] prowadząca przedmiot. Dlatego też pierwsze kolokwium wzbudza niesłychane emocje, a studenci porzucają piwo i dziewczyny, żeby zasiąść do książek nazywanych np. Geometria wykreślna. Podręcznik dla opornych. Napełnieni poczuciem wiedzy ruszają następnie na uczelnię celem napisania kolokwium. To zaś najczęściej utwierdza ich w przekonaniu, że wszystko jest łatwe. Bomba wybucha dopiero, gdy dochodzi do podania wyników prac. I w ogóle to czego pan jeszcze ode mnie chce? Tu jest taka plamka, o. A jej nie powinno być. To zaburza odbiór rysunku. I te rzuty jeszcze takie nieciekawe. Czternaście punktów[8] to i tak za dużo jak na taką brzydką pracę.
Zobacz też[edytuj • edytuj kod]
- teoria stożka (twierdzenie o połówce kieliszka)
- kwadratura koła
- sześcian
- …a jak nie masz wykreślnej na studiach, to może przynajmniej jest mechanika płynów?
Przypisy
- ↑ Rodzaj aksonometrii
- ↑ Autor był leniwy i użył narzędzia Szatana zamiast rysować ręcznie
- ↑ Inne przejawy tej megalomanii to choćby mechanika Lagrange'a czy algebra Boole'a
- ↑ Tak, nawet pozwalają korzystać z narzędzia do pisania!
- ↑ Jak to nie wiesz jak konstruować elipsę? To w podstawówce było...
- ↑ Tak, tu naprawdę jest błąd
- ↑ Ten przedmiot wykładają tylko niespełnieni architekci po sześćdziesiątce lub matematycy, którym całki pożarły mózg
- ↑ Na możliwe na przykład 33.