Teoria stożka: Różnice pomiędzy wersjami
Ja8czy coś (dyskusja • edycje) M (po co ten enter???) |
|||
| (Nie pokazano 35 wersji utworzonych przez 15 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{{medal}} |
|||
[[Grafika:3kielony2.jpg|thumb|right|300px|Kieliszki o budowie quasi-stożka]] |
|||
[[ |
[[Plik:Four shot glasses.jpg|thumb|200px|Kieliszki o budowie quasi-stożka]] |
||
'''Teoria |
'''Teoria stożka''' – matematyczny dowód na to, dlaczego tzw. „połówka” (kieliszka) połówką nie jest. |
||
==Wstęp i |
== Wstęp i założenia teoretyczne == |
||
Teoria stożka, zwana również alkoholową teorią stożka, jest pierwszym matematycznym dowodem na to, że tzw. połówka (słowo często używane w zwrocie: ''Nalej mi połówkę'') niekoniecznie połówką być musi. Zjawisko picia „połówek” występuje głównie u [[kobieta|kobiet]], rzadziej u [[mężczyzna|mężczyzn]] – dzięki teorii stożka pełny po brzegi [[kieliszek]] też jest połówką. Wynika to z budowy owego naczynia które jest często [[paraboloida obrotowa|paraboloidą obrotową]] – czyli w połowie wysokości tejże przestrzennej figury jest mniej niż połowa objętości, jaką można w tej figurze umieścić. |
|||
| ⚫ | |||
==Historia== |
|||
| ⚫ | |||
Twórcą teorii stożka jest Dariusz Wypiór znany jako Pikuś, który przy pomocy młodszego adiunkta wsparcia matematyki stosowanej w oparciu o jego dorobek [[nauka|naukowy]] Waldemara Kajdasa potwierdził słuszność i celowość tezy. Pierwszy publiczny odczyt miał miejsce w [[Ma%C5%82opolska|małopolskiej]] miejscowości [[Chocznia]] k/[[Wadowice|Wadowic]] w sierpniu 2005 roku. W krótkim czasie od pierwszego odczytu zostało powołanych kilka for dyskusyjnych, na których uczestnicy posługując się aparatem [[matematyka|matematycznym]] jak i empirycznym zgodzili się, a także potwierdziło teorie stożka. |
|||
| ⚫ | Do zobrazowania dowodu, który został przedstawiony poniżej, został przeprowadzony [[pomiar]] cech parametrycznych (wymiarów) kieliszka (quasi-stożka) o równoległych do siebie płaszczyznach dolnej (dna) i górnej. W teorii posługujemy się ściętym stożkiem, a nie paraboloidą obrotową, aby ułatwić zrozumienie zagadnienia – wyniki dla obu tych figur przestrzennych są niemal jednakowe. (Tworząc matematyczny obraz kieliszka jako stożka unikamy wprowadzania bardziej skomplikowanych [[wzór matematyczny|wzorów]]). |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Do zobrazowania dowodu, który został przedstawiony poniżej został przeprowadzony [[pomiar]] cech parametrycznych (wymiarów) kieliszka (quasi-stożka) o równoległych do siebie |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Zmierzone wartości przenosimy na dwuwymiarowy [[układ współrzędnych]]. Ważne jest, aby rysunek był zrobiony czytelnie i możliwie jak najdokładniej (Rys. 1). Otrzymując równanie tworzącej stożka <math>y=5x-4</math>. Jako, że współczynnik <math>a</math> jest wartością funkcji tangens kąta między osią <math>x</math>, a tworzącą, otrzymujemy kąt nachylenia tworzącej 78 stopni. |
||
| ⚫ | |||
| ⚫ | Zmierzone wartości przenosimy na dwuwymiarowy [[ |
||
Do dowodu przyjmujemy wysokość 9,5 cm gdzie: |
Do dowodu przyjmujemy wysokość 9,5 cm gdzie: |
||
* <0cm, 4cm) |
* <math>\langle 0cm, 4cm )</math> – nierzeczywiste przedłużenie stożka tzw. nóżka |
||
* <4cm, 9 |
* <math>\langle 4cm, 9.5cm \rangle</math> – stożek właściwy (mierzalny), tzw. komora wódkowa lub komora szczęścia |
||
==Dowód założeń teoretycznych== |
== Dowód założeń teoretycznych == |
||
[[ |
[[Plik:stozek3d2.jpg|thumb|200px|Rys. 2 – quasi-stożek; granice całkowania]] |
||
[[ |
[[Plik:granice3d2.jpg|thumb|200px|Rys. 3 – granice całkowania]] |
||
[[ |
[[Plik:granice2a3d2.jpg|thumb|200px|Rys. 4 – granice całkowania]] |
||
W dowodzie właściwym udowodnimy |
W dowodzie właściwym udowodnimy – groteskowo stwierdzając – że „połówka” występuje w każdym miejscu. gdzie osoba rozlewająca zachce tę „połówkę” mieć. A ściślej rzecz biorąc, formułujemy tezę: ''Połowa kieliszka mieści się miedzy jego połową wysokości a całą wysokością.'' |
||
Obliczamy objętość kieliszka (uwzględniając pomiary wyżej zebrane). Objętość V równa się całce potrójnej z jedności po obszarze D. Obszar D dzielimy na dwa: A oraz B. Obszar A składa się z obszarów D2,D4,D5 (Rys. 3) a B z D1,D3. Układ kartezjański zamieniamy na cylindryczny. |
Obliczamy objętość kieliszka (uwzględniając pomiary wyżej zebrane). Objętość <math>V</math> równa się całce potrójnej z jedności po obszarze <math>D</math>. Obszar <math>D</math> dzielimy na dwa: <math>A</math> oraz <math>B</math>. Obszar <math>A</math> składa się z obszarów <math>D2,D4,D5</math> (Rys. 3) a <math>B</math> z <math>D1,D3</math>. Układ kartezjański zamieniamy na cylindryczny. |
||
| ⚫ | |||
| ⚫ | |||
<math>0\leq\varphi\leq 2\pi</math> |
<math>0\leq\varphi\leq 2\pi</math> |
||
<math>0 |
<math>0.8\leq\rho\leq 1.9</math> |
||
<math>5 |
<math>5\rho\leq\varphi\leq 9.5</math> |
||
| ⚫ | |||
| ⚫ | |||
<math>V1=\iiint\limits_D 1 \;dx \;dy \;dz=\int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8}d\rho \int\limits^{9.5}_{5\rho} \rho dh</math> |
<math>V1=\iiint\limits_D 1 \;dx \;dy \;dz=\int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8}d\rho \int\limits^{9.5}_{5\rho} \rho dh</math> |
||
| Linia 48: | Linia 44: | ||
<math>\int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8} [\varphi h]_{5\rho}^{9.5} d\rho = \int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8} ({9.5\rho}-{5\rho^2}) d\rho=</math> |
<math>\int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8} [\varphi h]_{5\rho}^{9.5} d\rho = \int\limits^{2\pi}_0 d\varphi \int\limits^{1.9}_{0.8} ({9.5\rho}-{5\rho^2}) d\rho=</math> |
||
<math>= 2\pi[({{9.5*1.9^2} \over 2}-{{5*1.9^3} \over 3})-({{9.5*0.8^2} \over 2}-{{5*0.8^3} \over 3})]=22.2</math> |
<math>= 2\pi\left[ \left({{9.5*1.9^2} \over 2}-{{5*1.9^3} \over 3} \right)-\left({{9.5*0.8^2} \over 2}-{{5*0.8^3} \over 3}\right) \right]=22.2</math> |
||
| ⚫ | |||
| ⚫ | |||
<math>0\leq\varphi\leq 2\pi</math> |
<math>0\leq\varphi\leq 2\pi</math> |
||
<math>0\leq\rho\leq 0 |
<math>0\leq\rho\leq 0.8</math> |
||
<math>4\leq\varphi\leq 9 |
<math>4\leq\varphi\leq 9.5</math> |
||
| ⚫ | |||
| ⚫ | |||
<math>V2=\int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0}d\rho \int\limits^{9.5}_{4} \rho dh</math> |
<math>V2=\int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0}d\rho \int\limits^{9.5}_{4} \rho dh</math> |
||
<math>\int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0} [\varphi h]_{4}^{9.5} d\rho = \int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0} ({9.5\rho}-{4\rho}) d\rho = 2\pi[{{5.5\rho^2} \over 2}]_0^{0.8}=11.1</math> |
<math>\int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0} [\varphi h]_{4}^{9.5} d\rho = \int\limits^{2\pi}_0 d\varphi \int\limits^{0.8}_{0} ({9.5\rho}-{4\rho}) d\rho = 2\pi\left[{{5.5\rho^2} \over 2}\right]_0^{0.8}=11.1</math> |
||
| ⚫ | |||
| ⚫ | |||
<math>V=V1+V2=22.2+11.1=33.3ml</math>''' |
<math>V=V1+V2=22.2+11.1=33.3ml</math>''' |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
* <math>Vd<Vg</math> |
|||
| ⚫ | Pierwszy wniosek: Połówki nie są sobie równe, oraz wniosek drugi – kluczowy – połowa objętości jest zawarta na przedziale względem wysokości od jej połowy do całej wysokości <math>H</math>. Uwzględniając brak przyrządów pomiarowych (mierników) oraz błąd paralaksy ludzkiego oka udowodniliśmy tezę, iż nasza „połówka” jest zawarta na przedziale <<math>1/2H,H</math>> w naszym konkretnym badanym przypadku <math>\langle 6.75cm, 9.5cm \rangle</math>. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Dysponując aparatem matematycznym, a konkretnie rachunkiem całkowym, udowodniliśmy słuszność i prawdziwość tezy. Przedstawiona teoria dla samej matematyki i nauk pokrewnych nie jest ważna i istotna, lecz ma duże znaczenie społeczne. Bardzo dobrze sprawdza się tam, gdzie w określonej przestrzeni i w określonym czasie znajduje się wiele osób w celu [[libacja alkoholowa|zamierzonej konsumpcji]]. Należy brać pod uwagę, że teoria jest prawdziwa dla kieliszków w kształcie paraboloidy obrotowej lub stożka (kieliszki o tworzącej nachylonej pod kątem 0-30 stopni względem osi symetrii najlepiej nadają się do spożywania płynów). Dla kieliszków typowo cylindrycznych traci sens. |
||
| ⚫ | |||
| ⚫ | |||
- Vd<Vg |
|||
| ⚫ | Pierwszy wniosek: Połówki nie są sobie równe oraz wniosek drugi |
||
{{Fizyka}} |
|||
| ⚫ | |||
{{Matematyka}} |
|||
| ⚫ | Dysponując aparatem matematycznym a konkretnie rachunkiem całkowym udowodniliśmy słuszność i prawdziwość tezy. Przedstawiona teoria dla samej matematyki i nauk pokrewnych nie jest ważna i istotna, lecz ma duże znaczenie społeczne. Bardzo dobrze sprawdza się tam gdzie w określonej przestrzeni i w określonym czasie znajduje się wiele osób w celu zamierzonej konsumpcji. Należy brać pod uwagę, że teoria jest prawdziwa dla kieliszków w kształcie paraboloidy obrotowej lub stożka ( |
||
[[Kategoria: |
[[Kategoria:Fizyka]] |
||
[[Kategoria:Geometria]] |
|||
Aktualna wersja na dzień 07:44, 11 lip 2023
Teoria stożka – matematyczny dowód na to, dlaczego tzw. „połówka” (kieliszka) połówką nie jest.
Wstęp i założenia teoretyczne[edytuj • edytuj kod]
Teoria stożka, zwana również alkoholową teorią stożka, jest pierwszym matematycznym dowodem na to, że tzw. połówka (słowo często używane w zwrocie: Nalej mi połówkę) niekoniecznie połówką być musi. Zjawisko picia „połówek” występuje głównie u kobiet, rzadziej u mężczyzn – dzięki teorii stożka pełny po brzegi kieliszek też jest połówką. Wynika to z budowy owego naczynia które jest często paraboloidą obrotową – czyli w połowie wysokości tejże przestrzennej figury jest mniej niż połowa objętości, jaką można w tej figurze umieścić.
Pomiar szkliwa (kieliszka)[edytuj • edytuj kod]
Do zobrazowania dowodu, który został przedstawiony poniżej, został przeprowadzony pomiar cech parametrycznych (wymiarów) kieliszka (quasi-stożka) o równoległych do siebie płaszczyznach dolnej (dna) i górnej. W teorii posługujemy się ściętym stożkiem, a nie paraboloidą obrotową, aby ułatwić zrozumienie zagadnienia – wyniki dla obu tych figur przestrzennych są niemal jednakowe. (Tworząc matematyczny obraz kieliszka jako stożka unikamy wprowadzania bardziej skomplikowanych wzorów).
- Wysokość:
- Promień podstawy dolnej:
- Promień podstawy górnej:
Do dalszych obliczeń błąd miernika (w tym wypadku linijki) nie będzie uwzględniany, gdyż zarówno ten błąd jak i odchyłka od wartości średniej pomiaru jest stosunkowo bardzo mała od spodziewanych wyników i nie wpływa na ostateczny wynik.
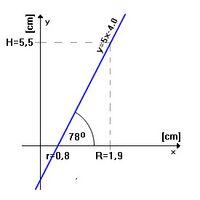
Zmierzone wartości przenosimy na dwuwymiarowy układ współrzędnych. Ważne jest, aby rysunek był zrobiony czytelnie i możliwie jak najdokładniej (Rys. 1). Otrzymując równanie tworzącej stożka . Jako, że współczynnik jest wartością funkcji tangens kąta między osią , a tworzącą, otrzymujemy kąt nachylenia tworzącej 78 stopni.
Do dowodu przyjmujemy wysokość 9,5 cm gdzie:
- – nierzeczywiste przedłużenie stożka tzw. nóżka
- – stożek właściwy (mierzalny), tzw. komora wódkowa lub komora szczęścia
Dowód założeń teoretycznych[edytuj • edytuj kod]
W dowodzie właściwym udowodnimy – groteskowo stwierdzając – że „połówka” występuje w każdym miejscu. gdzie osoba rozlewająca zachce tę „połówkę” mieć. A ściślej rzecz biorąc, formułujemy tezę: Połowa kieliszka mieści się miedzy jego połową wysokości a całą wysokością.
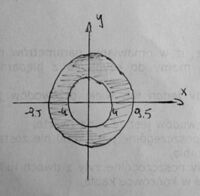
Obliczamy objętość kieliszka (uwzględniając pomiary wyżej zebrane). Objętość równa się całce potrójnej z jedności po obszarze . Obszar dzielimy na dwa: oraz . Obszar składa się z obszarów (Rys. 3) a z . Układ kartezjański zamieniamy na cylindryczny.
Zamiana na zmienne walcowe po obszarze :
Rozwiązanie całki:
Zamiana na zmienne walcowe po obszarze :
Rozwiązanie całki:
Sumaryczna objętość mierzonego quasi-stożka (kieliszka) wynosi:
Połowa wysokości kieliszka znajduje się na wysokości . W sposób analogiczny do przedstawionego powyżej obliczamy objętość połówki dolnej (po obszarach ) oraz połówki górnej () otrzymując:
- Objętość połówki dolnej:
- Objętość połówki górnej:
Pierwszy wniosek: Połówki nie są sobie równe, oraz wniosek drugi – kluczowy – połowa objętości jest zawarta na przedziale względem wysokości od jej połowy do całej wysokości . Uwzględniając brak przyrządów pomiarowych (mierników) oraz błąd paralaksy ludzkiego oka udowodniliśmy tezę, iż nasza „połówka” jest zawarta na przedziale <> w naszym konkretnym badanym przypadku .
Uwagi[edytuj • edytuj kod]
Dysponując aparatem matematycznym, a konkretnie rachunkiem całkowym, udowodniliśmy słuszność i prawdziwość tezy. Przedstawiona teoria dla samej matematyki i nauk pokrewnych nie jest ważna i istotna, lecz ma duże znaczenie społeczne. Bardzo dobrze sprawdza się tam, gdzie w określonej przestrzeni i w określonym czasie znajduje się wiele osób w celu zamierzonej konsumpcji. Należy brać pod uwagę, że teoria jest prawdziwa dla kieliszków w kształcie paraboloidy obrotowej lub stożka (kieliszki o tworzącej nachylonej pod kątem 0-30 stopni względem osi symetrii najlepiej nadają się do spożywania płynów). Dla kieliszków typowo cylindrycznych traci sens.






















![{\displaystyle \int \limits _{0}^{2\pi }d\varphi \int \limits _{0.8}^{1.9}[\varphi h]_{5\rho }^{9.5}d\rho =\int \limits _{0}^{2\pi }d\varphi \int \limits _{0.8}^{1.9}({9.5\rho }-{5\rho ^{2}})d\rho =}](https://nonsa.pl/api/rest_v1/media/math/render/svg/a95cc387b596f1850ee4d5c4ef172753f7c3c753)
![{\displaystyle =2\pi \left[\left({{9.5*1.9^{2}} \over 2}-{{5*1.9^{3}} \over 3}\right)-\left({{9.5*0.8^{2}} \over 2}-{{5*0.8^{3}} \over 3}\right)\right]=22.2}](https://nonsa.pl/api/rest_v1/media/math/render/svg/e44dba90e7247e66d7c829d86f1cd7ee658943aa)



![{\displaystyle \int \limits _{0}^{2\pi }d\varphi \int \limits _{0}^{0.8}[\varphi h]_{4}^{9.5}d\rho =\int \limits _{0}^{2\pi }d\varphi \int \limits _{0}^{0.8}({9.5\rho }-{4\rho })d\rho =2\pi \left[{{5.5\rho ^{2}} \over 2}\right]_{0}^{0.8}=11.1}](https://nonsa.pl/api/rest_v1/media/math/render/svg/64b283b4f59d9bba33e47e8872758df85768e815)












